进制
常用进制
- 二进制 binary system
- 八进制 octonary number system 、octal、O
- 十进制 decimalism
- 十六进制 hexadecimal、hex、0x
二进制表示
机器数
一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机中用一个数的最高位存放符号, 正数为0, 负数为1。比如,十进制中的数+3,计算机字长为8位,转换成二进制就是 00000011 。这里的 00000011 就是机器数。
真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。例如有符号数 10000011,其最高位1代表负,其真正数值是 -3 而不是形式值131(10000011转换成十进制等于131)。所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。例:0000 0001的真值是 1,1000 0001的真值是 –1。
将一个真值表示成二进制字串的机器数的过程就称为编码。
原码
原码就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值。比如,如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位。因为第一位是符号位,所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
[-127 , 127]
原码是人脑最容易理解和计算的表示方式
反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上,符号位不变,其余各个位取反。
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数,人脑无法直观的看出来它的数值, 通常要将其转换成原码再计算。
补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1,即在反码的基础上+1。
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数,补码表示方式也是人脑无法直观看出其数值的,通常也需要转换成原码在计算其数值.
源码、反码、补码
正数:
原码=反码=补码
负数:
- 反码=原码的所有位(符号位除外)取反
- 补码=反码+1
一个字节为什么存的值是-128到127,int取值范围怎么算的?
一个字节的取值范围为什么是-128~127呢?
一个字节有8位,第1位是符号位,1代表负数,0代表正数。
所以一个字节:
最小正数二进制是0000 0000=0
最大正数二进制是0111 1111 = 64+32+16+8+4+2+1=127
最大负数二进制是1111 1111 = -1
最小负数二进制是1000 0000→ 反码:1111 1111→ 补码: - {(1+2+4+8+16+32+64)+1} =-(127+1)=-128
8位一共存储2^8=256个数,由于计算机中0没有正负之分,所以存的数值为:-128 —— -1 和 0 —— 127
int取值范围:p
int占四个字节,32位
| 数据 | 十进制 | 十六进制 | 二进制 |
|---|---|---|---|
| 最小正数 | 0 | 0 | 0000 0000 0000 0000 0000 0000 0000 0000 |
| 最大正数 | 2147483647 | 7FFF FFFF | 0111 1111 1111 1111 1111 1111 1111 1111 |
| 最小负数 | -2147483648 | 8000 0000 | 1000 0000 0000 0000 0000 0000 0000 0000 |
| 最大负数 | -1 | 7FFF FFFF | 1111 1111 1111 1111 1111 1111 1111 1111 |
原码、反码、补码是计算机中表示数值的三种不同编码方式,以下是它们的详细介绍:
- 原码
- 定义:原码是一种简单的机器数表示法,最高位为符号位,0 表示正数,1 表示负数,其余位表示数值的绝对值。
- 示例:以 8 位二进制数为例,+7 的原码是 00000111,-7 的原码是 10000111。
- 特点:原码的优点是直观易懂,与人们日常的数值表示方式相似。但它的缺点是在进行加减法运算时,需要根据符号位来判断运算规则,增加了运算的复杂性。
- 反码
- 定义:对于正数,其反码与原码相同;对于负数,其反码是在原码的基础上,除符号位外,其余各位按位取反。
- 示例:以 8 位二进制数为例,+7 的反码是 00000111,-7 的反码是 11111000。
- 特点:反码在计算机中主要作为原码到补码转换的中间过渡形式,本身使用相对较少。它解决了原码在符号位处理上的一些问题,但仍存在一些不足,如 0 的表示不唯一等。
- 补码
- 定义:对于正数,其补码与原码相同;对于负数,其补码是在反码的基础上,末位加 1。
- 示例:以 8 位二进制数为例,+7 的补码是 00000111,-7 的补码是 11111001。
- 特点:补码的引入主要是为了解决原码在加减法运算中的复杂性问题。在补码表示下,符号位可以像数值位一样参与运算,使得加减法运算可以统一进行,大大简化了计算机的运算电路设计。而且,补码中 0 的表示是唯一的。
在计算机中,通常使用补码来表示有符号整数,因为它能够方便地进行数值的存储和运算,提高了计算机处理数据的效率和准确性。
原码、反码和补码之间如何进行转换?
原码、反码和补码之间的转换规则如下(以 8 位二进制数为例):
1. 正数的转换
规则:正数的原码、反码、补码完全相同,符号位为 0,数值位为真值的二进制表示。
示例:以 +7 为例
- 原码:
0 0000111符号位0,数值位0000111(即十进制的 7)。 - 反码:
0 0000111与原码相同。 - 补码:
0 0000111与原码相同。
2. 负数的转换
规则:
- 原码 → 反码:符号位不变(仍为
1),数值位按位取反(0变1,1变0)。 - 反码 → 补码:在反码的基础上,末位加
1。 - 补码 → 原码:先对补码减
1得到反码,再对反码取反得到原码(符号位始终不变)。
示例:以 -7 为例
- 原码:
1 0000111符号位1,数值位0000111。 - 反码:
1 1111000符号位不变,数值位取反。 - 补码:
1 1111001反码末位加1。
补码 → 原码的验证:
- 补码
1 1111001 - 减
1得反码:1 1111000 - 数值位取反得原码:
1 0000111(即-7)。
3. 特殊值 0 的表示
规则:
原码
:有两种表示方式:
+0:0 0000000-0:1 0000000
反码
:同样有两种表示方式:
+0:0 0000000-0:1 1111111
补码
:只有一种表示方式:
0:0 0000000(原码的-0在补码中表示为-128)
4. 示例:求 -128 的补码(8 位)
步骤:
原码:无法用 8 位原码表示(原码范围为
-127到+127)。补码
:直接计算:
- 超出原码范围的数(如
-128)的补码为10000000。 - 验证:补码
10000000减1得01111111(反码),取反得10000000(原码形式,但在补码中解释为-128)。
- 超出原码范围的数(如
5. 总结转换公式
| 原码 → 补码 | 补码 → 原码 |
|---|---|
| 正数:不变 | 正数:不变 |
| 负数:数值位取反 +1 | 负数:数值位取反 +1 |
记忆技巧
- 正数:三码合一。
- 负数:原码 ↔ 补码 互为 “取反加 1”。
- 补码优势:统一加减法运算,符号位可直接参与计算。
掌握这些规则后,即可快速进行原码、反码和补码之间的转换。
原码、反码和补码分别是如何被应用在计算机中的?
原码、反码和补码在计算机中有不同的应用方式,具体如下:
原码
- 简单数据表示:原码直接表示数值的大小和符号,直观地反映了数值的真实情况,常用于一些对数值表示精度要求不高,且更注重直观理解的场景,如在计算机早期的一些简单数据处理程序中,或在一些需要直接展示数值原始形态的调试工具中,开发人员可以通过原码清晰地看到数值的符号和绝对值部分。
- 乘法运算:在计算机乘法运算中,原码可用于部分计算过程。因为原码的符号位可以直接参与符号的判断,根据两个数的符号位异或来确定乘积的符号,而数值部分则可以按照普通的乘法规则进行运算,最后再将符号位和数值部分组合得到结果的原码。
反码
- 作为中间过渡:反码主要作为原码到补码转换的中间步骤。在计算机内部进行数据处理和运算时,当需要将原码转换为补码进行运算,或者在某些需要对补码进行逆向操作得到原码的情况下,反码就起到了过渡的作用,帮助完成这些转换过程。
- 早期计算机运算探索:在计算机发展的早期阶段,也曾尝试过使用反码进行一些运算,但由于反码存在一些缺陷,如 0 的表示不唯一等问题,导致其在实际运算中的应用不够理想,逐渐被补码所取代,但在一些特定的历史资料或早期计算机体系结构的研究中,仍能看到反码在运算中的相关应用。
补码
- 数据存储:计算机中通常使用补码来存储有符号整数。因为补码可以将正数和负数统一表示,并且 0 的表示唯一,使得计算机在存储和处理数值数据时更加方便和高效。例如,在 8 位二进制补码表示中,
00000000表示0,10000000表示-128,01111111表示127,这样可以充分利用所有的二进制组合来表示不同的数值,扩大了可表示的数值范围。 - 加减法运算:补码的最大优势在于可以将加减法运算统一起来。在计算机的运算器中,无论是加法还是减法,都可以通过补码的加法来实现。例如,计算
5 - 3,可以转化为5 + (-3),5的补码是00000101,-3的补码是11111101,将它们相加得到00000010,即2的补码,结果正确。这样就大大简化了计算机运算电路的设计,提高了运算效率。 - 实现模运算:在一些需要进行模运算的场景中,补码也有重要应用。例如,在计算机的时钟系统中,通过补码可以方便地实现对时间的循环计数,就像时钟在 12 点之后又从 1 点开始计数一样,利用补码可以实现类似的循环计数机制,以处理各种周期性的数据。
https://www.doubao.com/thread/w7206ac974b710cff
定点数
定点数是小数点固定的数。在计算机中没有专门表示小数点的位,小数点的位置是约定默认的。一般固定在机器数的最低位之后,或是固定在符号位之后。前者称为定点纯整数,后者称为定点纯小数。定点数表示法简单直观,但是数值表示的范围太小,运算时容易产生溢出。
浮点数
浮点数是小数点的位置可以变动的数。为增大数值表示范围,防止溢出,采用浮点数表示法。浮点表示法类似于十进制中的科学计数法。
在计算机中通常把浮点数分成阶码和尾数两部分来表示,其中阶码一般用补码定点整数表示,尾数一般用补码或原码定点小数表示。为保证不损失有效数字,对尾数进行规格化处理,也就是平时所说的科学记数法,即保证尾数的最高位为1,实际数值通过阶码进行调整。
阶符表示指数的符号位、阶码表示幂次、数符表示尾数的符号位、尾数表示规格化后的小数值。
N = 尾数×基数阶码(指数)
作用
计算机可以有三种编码方式表示一个数,接下来说下原码、补码、反码的作用。
对于正数
[+1] = [00000001]原 = [00000001]反 = [00000001]补
三种编码方式的结果都相同
对于负数
[-1] = [10000001]原 = [11111110]反 = [11111111]补
二进制的负数用补码表示
可见原码、反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式,为何还会有反码和补码呢?
首先,因为人脑可以知道第一位是符号位,在计算的时候我们会根据符号位,选择对真值区域的加减。但是对于计算机,加减乘数已经是最基础的运算,要设计的尽量简单,计算机辨别符号位显然会让计算机的基础电路设计变得十分复杂!
于是人们想出了将符号位也参与运算的方法。我们知道,根据运算法则减去一个正数等于加上一个负数,即:1-1 = 1 + (-1) = 0, 所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。
于是人们开始探索将符号位参与运算,并且只保留加法的方法。首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示,让符号位也参与计算,显然对于减法来说,结果是不正确的,这也就是为何计算机内部不使用原码表示一个数。
为了解决原码做减法的问题,出现了反码:
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法,结果的真值部分是正确的,而唯一的问题其实就出现在0这个特殊的数值上。虽然人们理解上+0和-0是一样的,但是0带符号是没有任何意义的,而且会有[0000 0000]原和[1000 0000]原两个编码表示0,很浪费。
于是补码的出现,解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
总结
反码是为了解决减法运算。
补码是为了解决反码产生的±0的问题。
补充
[0000 0001]补 + [1111 1111] 补结果是会溢出的,计算时都要溢出的,否则计算就会错误,补码也就没意义了。
这样0用[0000 0000]表示,而以前出现问题的-0则不存在了,而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128,在用补码运算的结果中,[1000 0000]补码就是-128。但是注意因为实际上是使用以前的-0的补码来表示-128,所以-128并没有原码和反码表示。对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原,这是不正确的。
因为机器使用补码,所以对于编程中常用到的32位int类型,可以表示范围是:[-231, 231-1] ,因为第一位表示的是符号位,而使用补码表示时又可以多保存一个最小值。
另如:8位类型原码:[11111111] - [01111111],即-127 - 127,但补码能多表示一个最小值(原码反码补码都是不同的表示方式,但最终的真值是一样的),即8位类型数据可以表示的范围为:-128 - 127。
16位即[-215, 215-1],32位即[-231, 231-1]
常用位数的边界值
8位无符号整数范围
[0 - 28-1],即[0 - 255]或[0 - 0xFF]
16位无符号整数范围
[0 - 216-1],即[0 - 65535]或[0 - 0xFFFF]
32位无符号整数范围
[0 - 232-1],即[0 - 4294967295]或[0 - 0xFFFFFFFF]
8位有符号整数范围
[-27- 27-1],即[-128 - 127]或[-0x80 - 0x7F]
16位有符号整数范围
[-215 - 215-1],即[-32768 - 32767]或[0x8000 - 0x7FFF]
32位有符号整数范围
[-231 - 231-1],即[-2147483648- 2147483647]或[0x80000000 - 0x7FFFFFFF]
长整数与短整数转换
短整数转长整数补符号为即可 原来8位如果符号是1前面补8个1,如果符号是0前面补8个0
长整数转短整数,计算机会把前面8位砍掉,则发生精度丢失需要注意
LITTLE ENDIAN / BIG ENDIAN (不重要)
大端与小端:超过一个字节的数在内存中的存储顺序
低位在内存小地址 LITTLE ENDIAN
高位在内存小地址 BIG ENDIAN
位掩码
是一种运用位运算的技巧, linux的权限系统就是使用位掩码来构建的,权限掩码umask(umask用来设置默认权限的)。
在设计一个权限系统的时候往往免不了四种权限: 增删改查, 如果我们为每种有可能出现的权限都写一个变量来标识, 那我们需要写 2 ^ 4 = 16 个变量还储存这些组合.
这时就可以用位运算来优化, 首先我们用四个变量来表示权限:
const Insert = 1 // 0001
const Delete = 2 // 0010
const Update = 4 // 0100
const Select = 8 // 1000
比如我们想给一个用户添加 Insert 权限, 那怎么添加呢?
只需要用 |运算符:
const user = registerUser(data)
// 初始为 0000
user.premission = 0
// 如果想新增一个权限 0000 | 0001 => 0001, 此时就拥有了 Insert 的权限
user.premission = user.premission | Insert
// 如果想在增加一个权限 0001 | 0010 => 0011, 此时就拥有了 Insert,Delete 权限
user.premission = user.premission | Delete
// 如果想在增加一个权限 0011 | 0100 => 0111, 此时就拥有了 Insert,Delete,Update 权限
user.premission = user.premission | Update
此时肯定有小伙伴心里在想 0011 不是 3 吗, 我怎么知道 3 有没有包含 Insert 和 Delete 权限嘞?
只需要用 &运算符:
// 0011 & 0010 => 0010 也就是 Delete 的权限
user.premission & Delete === Delete
// 用户权限去 & 指定权限的结果等于指定权限, 那么就意味着该用户拥有该权限.
在用户有 Delete 和 Insert 的同时, 我们怎么取出其中的一个
只需要用 ^运算符:
// 0011 ^ 0010 => 0001
user.premission ^ Delete === Insert
如何删除权限?
需要用到 & 和 ~
// 有 Delete 和 Insert 权限
0011 & ~ 0001
↓ 取反 补码 十进制
1. 先做 ~ 0001, 这里我们只到补码部分 ~ 0 0001 => 1 1110 => 1 0010 => -2
2. 转换 0011 到补码形式 -> 0 0011
3. 0011 & 0010 => 0010 => 2
user.premission = user.premission & ~ Insert === Delete
移码?
进制转换
转二进制
- 正整数转二进制
- 负整数转二进制
- 小数转二进制
正整数转二进制
正整数转成二进制。要点一定一定要记住哈:除二取余,然后倒序排列,高位补零。也就是说,将正的十进制数除以二,得到的商再除以二,依次类推知道商为零或一时为止,然后在旁边标出各步的余数,最后倒着写出来,高位补零。比如42转换为二进制,如图所示操作。
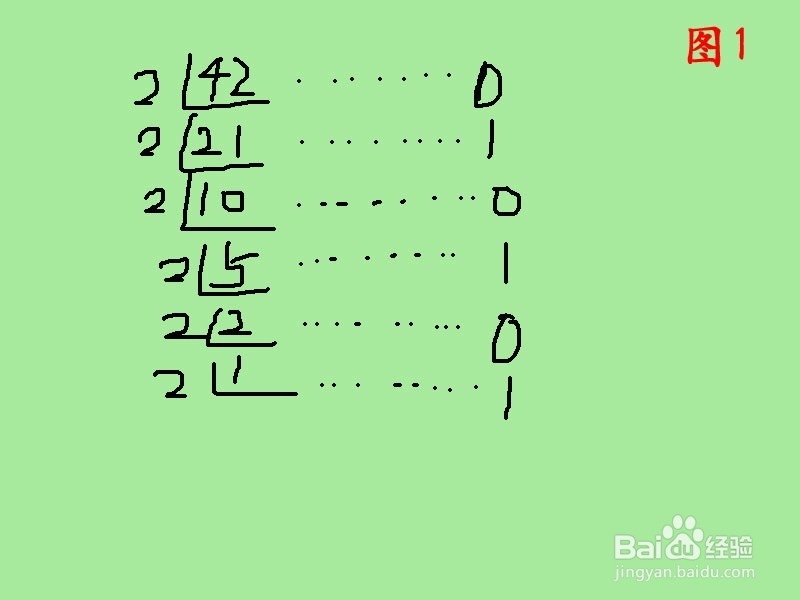
42除以2得到的余数分别为010101,然后咱们倒着排一下,42所对应二进制就是101010.如图所示更直观的表达。
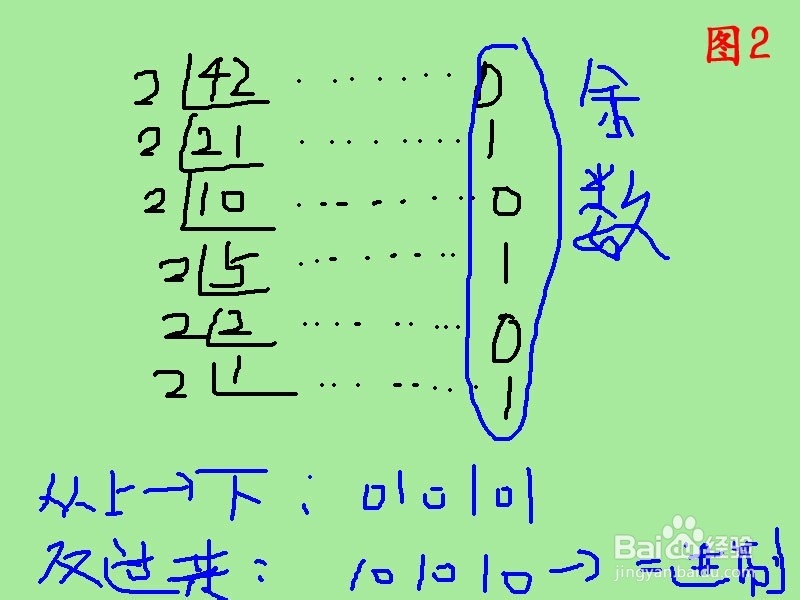
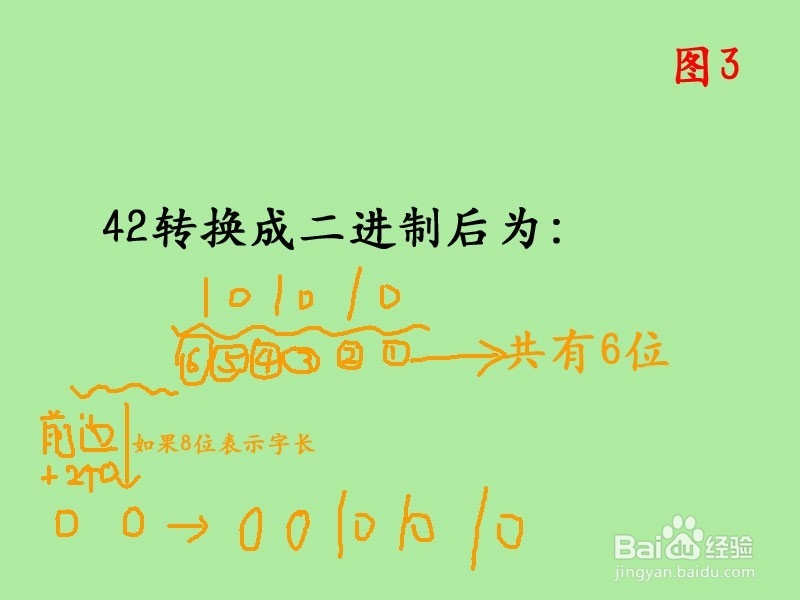
计算机内部表示数的字节单位是定长的,如8位,16位,或32位。所以,位数不够时,高位补零,所说,如图所示,42转换成二进制以后就是。00101010,也即规范的写法为(42)10=(00101010)。
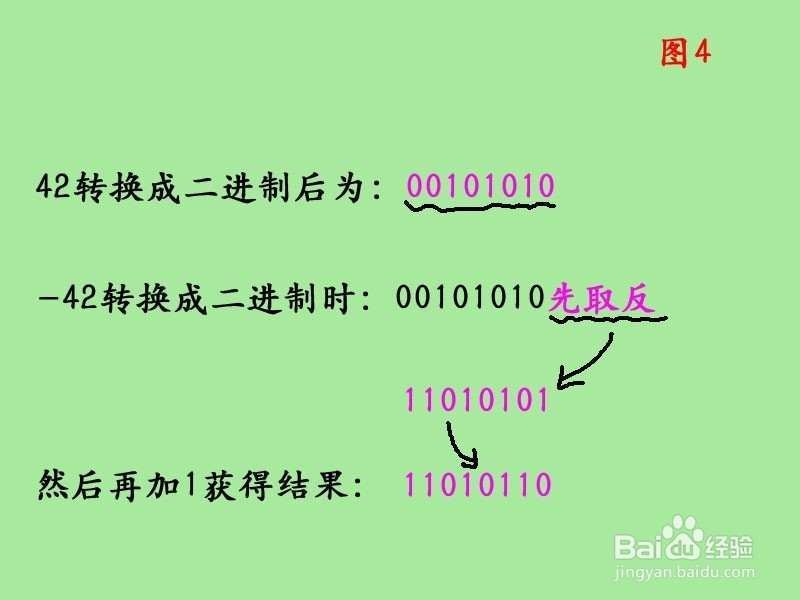
负整数转换成二进制
先是将对应的正整数转换成二进制后,对二进制取反,然后对结果再加一。还以42为例,负整数就是-42,如图所示为方法解释。最后即为:(-42)10=(11010110)
小数转二进制
对小数点以后的数乘以2,有一个结果吧,取结果的整数部分(不是1就是0喽),然后再用小数部分再乘以2,再取结果的整数部分……以此类推,直到小数部分为0或者位数已经够了。然后把取的整数部分按先后次序排列,就构成了二进制小数部分的序列,举个例子吧,比如0.125,如图所示。

如果小数的整数部分有大于0的整数时该如何转换呢?如以上整数转换成二进制,小数转换成二进制,然后加在一起,如图所示。

整数二进制转换为十进制:首先将二进制数补齐位数,首位如果是0就代表是正整数,如果首位是1则代表是负整数。
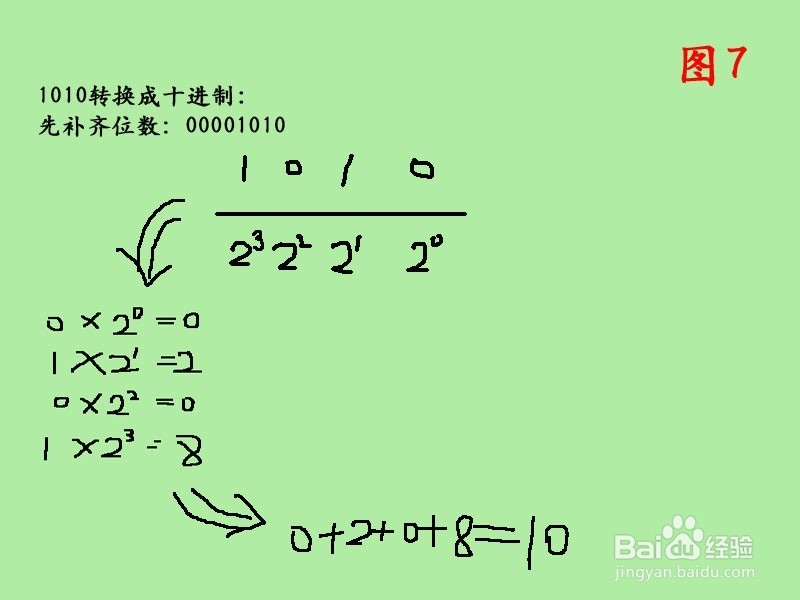
先看首位是0的正整数,补齐位数以后,将二进制中的位数分别将下边对应的值相乘,然后相加得到的就为十进制,比如1010转换为十进制,方法如图所示。
若二进制补足位数后首位为1时,就需要先取反再换算:例如,11101011,首位为1,那么就先取反吧:-00010100,然后算一下10100对应的十进制为20,所以对应的十进制为-20,方法如图所示。

将有小数的二进制转换为十进制时:例如0.1101转换为十进制的方法:将二进制中的四位数分别于下边,如图所示,对应的值相乘后相加得到的值即为换算后的十进制。

进制之间转换
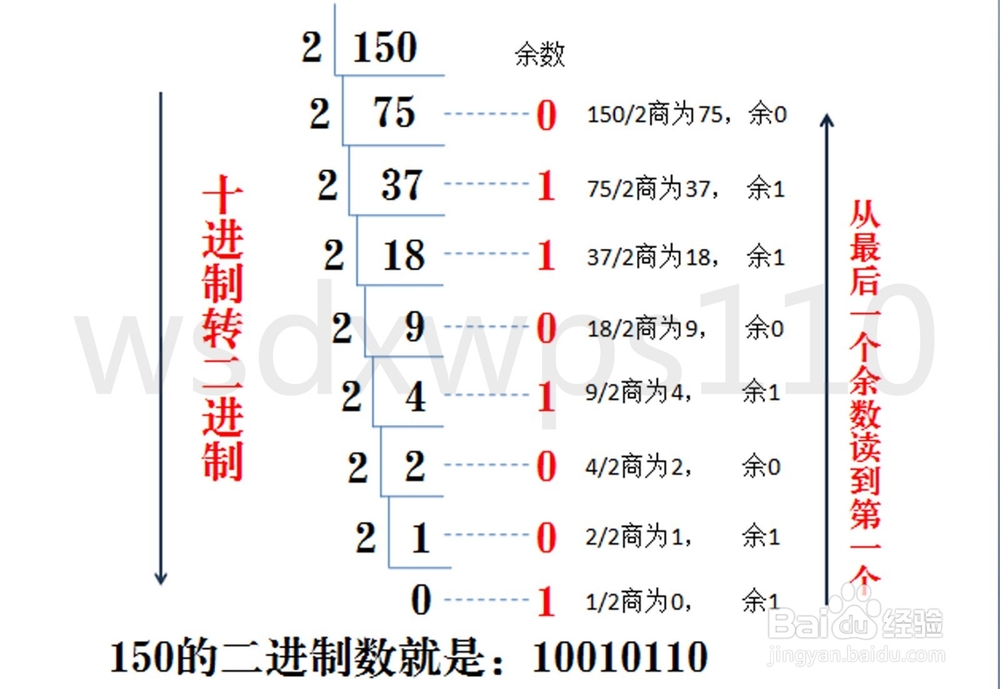
十进制转二进制
十进制数除2取余法,即十进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运算直到商为0为止。
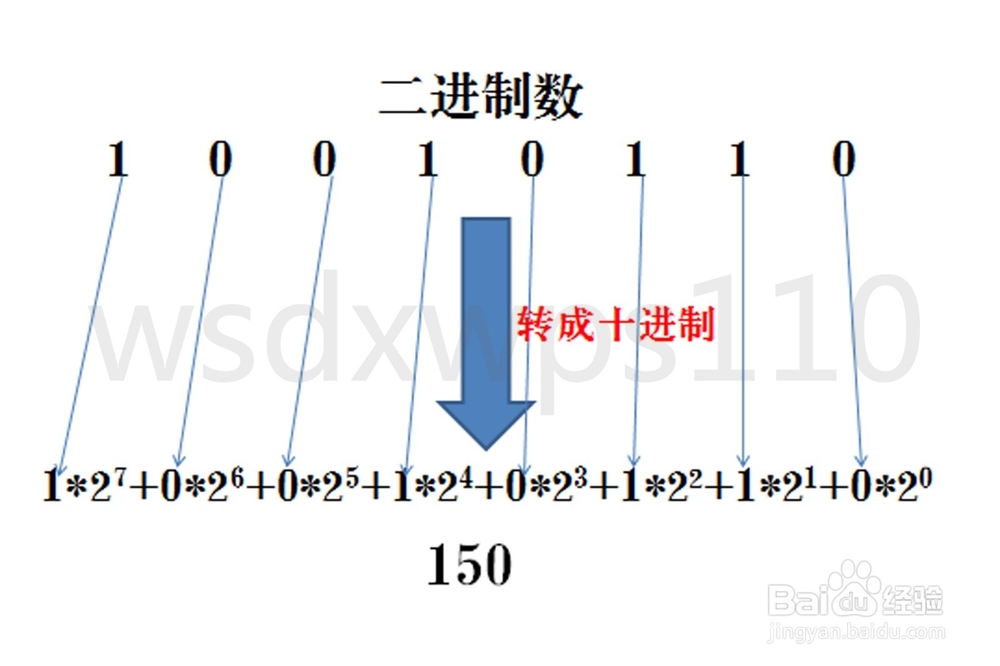
二进制转十进制
把二进制数按权展开、相加即得十进制数。
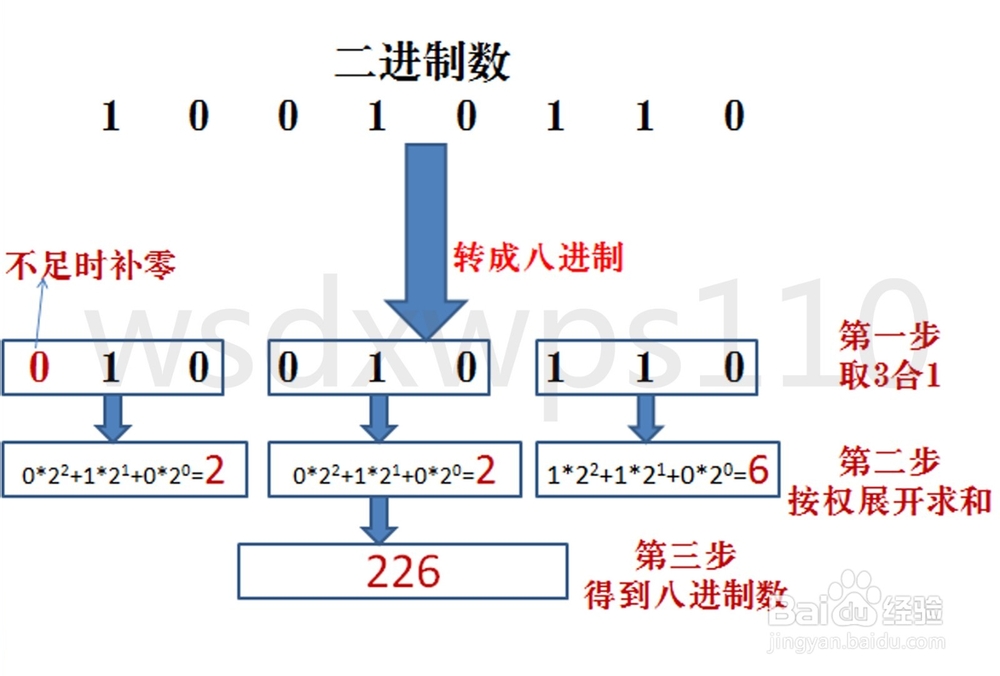
二进制转八进制
3位二进制数按权展开相加得到1位八进制数。(注意事项,3位二进制转成八进制是从右到左开始转换,不足时补0)。
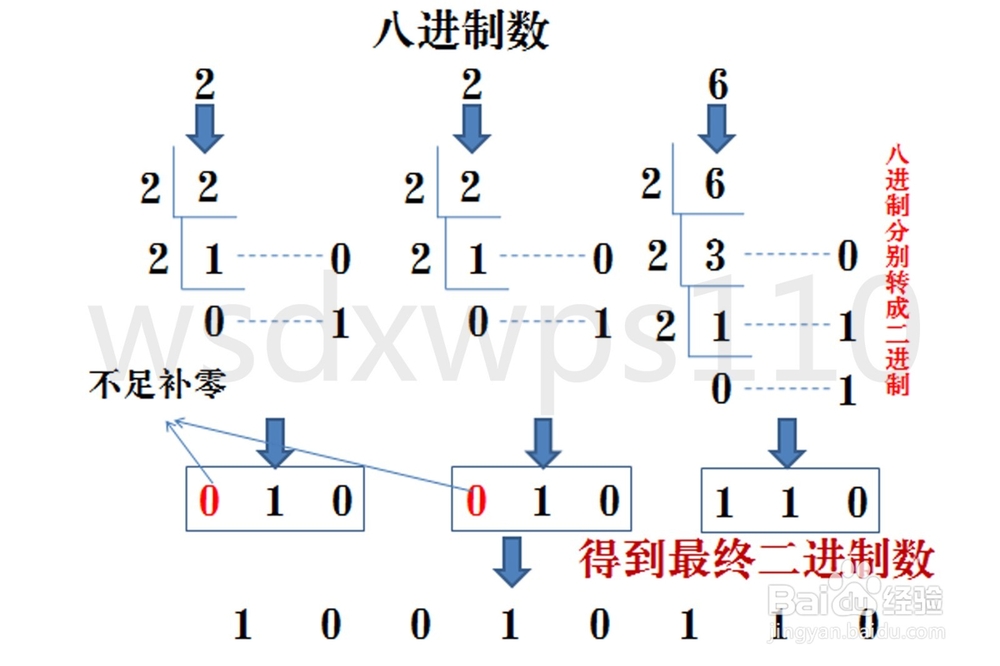
八进制转成二进制
八进制数通过除2取余法,得到二进制数,对每个八进制为3个二进制,不足时在最左边补零。
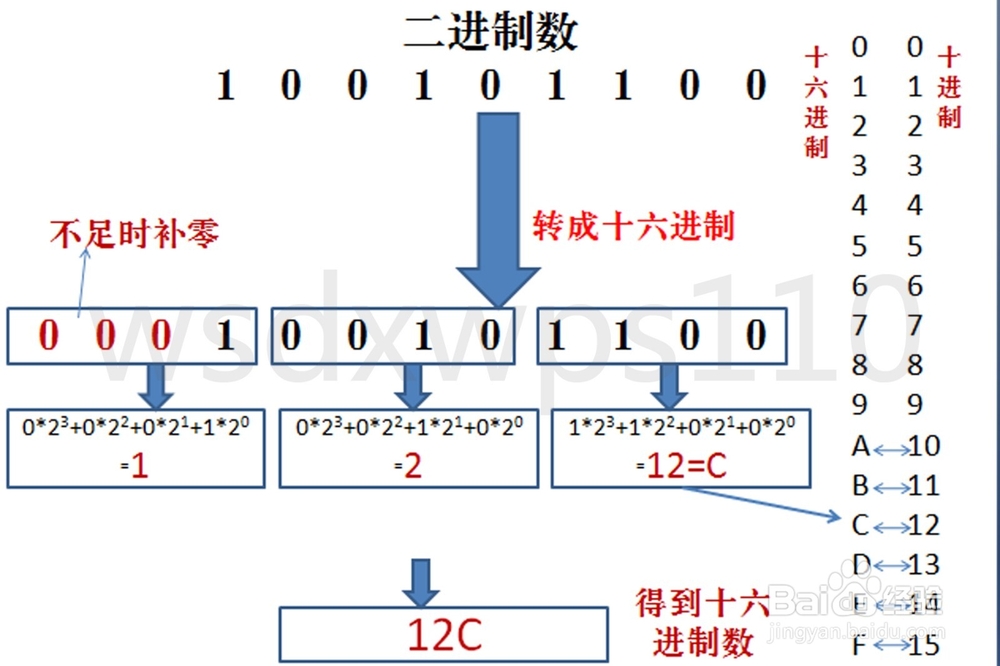
二进制转十六进制
与二进制转八进制方法近似,八进制是取三合一,十六进制是取四合一。(注意事项,4位二进制转成十六进制是从右到左开始转换,不足时补0)。
十六进制转二进制
十六进制数通过除2取余法,得到二进制数,对每个十六进制为4个二进制,不足时在最左边补零。

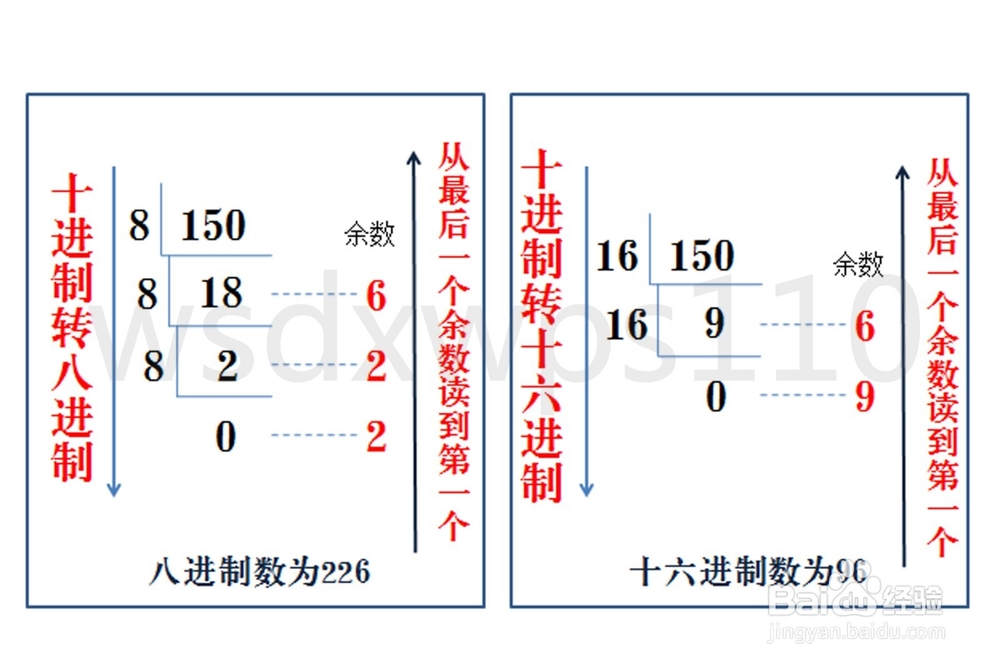
十进制转八进制或者十六进制有两种方法
间接法—把十进制转成二进制,然后再由二进制转成八进制或者十六进制。
直接法—把十进制转八进制或者十六进制按照除8或者16取余,直到商为0为止。
八进制或者十六进制转成十进制
- 把八进制、十六进制数按权展开、相加即得十进制数。
